# 18/01/21 - Predicting T20 Cricket Matches With a Ball Simulation Model
This article was originally published on Towards Data Science (opens new window).
'Tis the season to be watching lots of cricket and once again I have obliged. Yes, every summer I plonk myself down on the lounge and observe approximately seven million hours of my favourite sport, but last year I decided to spend some of the time between overs working on a predictive model. Modelling sports is a passion of mine and was actually the gateway drug that initially got me interested in data science. In the past, I have trained models to predict the outcomes of rugby matches, tennis matches and horse races and even won a lucrative first prize in a data science competition to predict the Australian Open.
My primary goal with this project was not to build the most accurate algorithm ever (nice as that would be) but rather to experiment with a probabilistic, bottom-up approach to modelling. Instead of trying to predict match results based on historical data, I trained a neural-network model to predict the outcome of individual balls and then built a custom Monte Carlo simulation engine to generate tens of thousands of possible games.

# Data
For this project, I used data on 677291 balls bowled in 3651 T20 matches involving 2255 players. The games took place between 2003 and 2020 and come from the following 7 leagues:
- Indian Premier League
- Big Bash League (Australia)
- Caribbean Premier League
- T20 Blast (England)
- Mzansi Super League (South Africa)
- Pakistan Super League
- Bangladesh Premier League
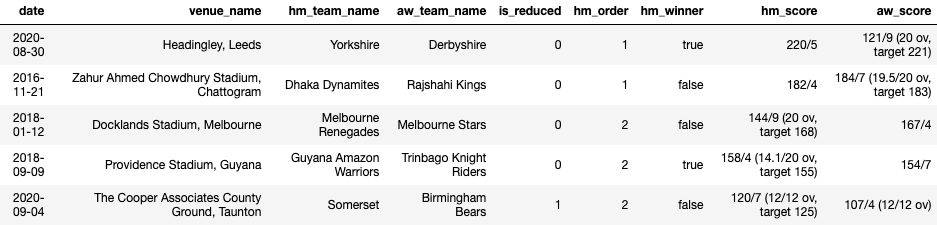
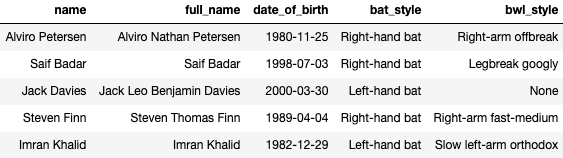
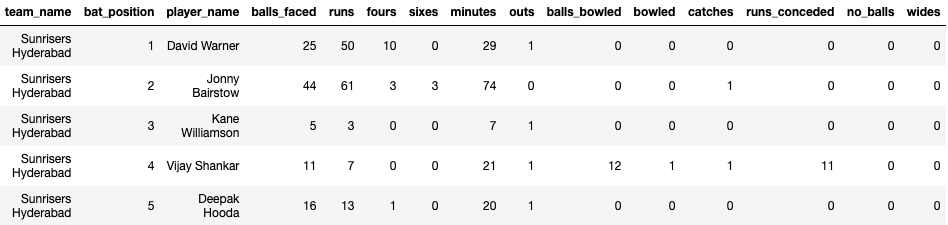
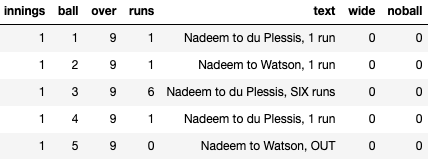
Unfortunately, I can't share the data source for this project since I leveraged my personal sports database but this kind of data is quite easy to find publicly. Below are some samples from my starting tables to give an idea of the kind of data I was working with.
# Match
# Player
# Player Match Statistics
# Commentary
# Approach
# Rationale
For this project, I decided to use a bottom-up approach by training a model to predict the outcome of each ball bowled (rather than the overall match result). My reasons were as follows:
- Head to head battles are a key part of cricket and this methodology allowed me to capture the matchups between individual batsmen and bowlers.
- Cricket matches are often decided by a few pivotal moments and the outcome of a single ball can have a huge impact on a result. The difference between a good or bad ball can be a matter of centimetres (e.g. a catch being taken on the boundary vs clearing the rope for six) but by simulating a match thousands of times we can approach these events probabilistically.
- It allows us to answer more complex questions (e.g. who is likely to take the most wickets in a match). A traditional top-down model can only make predictions about the specific task it was trained on (i.e. who will win a given match).
- We can get conditional probabilities of results e.g.:
- What is the probability of the Chennai Super Kings winning, given they batted first and scored 167 runs?
- What is the probability of the Brisbane Heat winning if Chris Lynn scores less than 20 runs?
# Ball Prediction Model
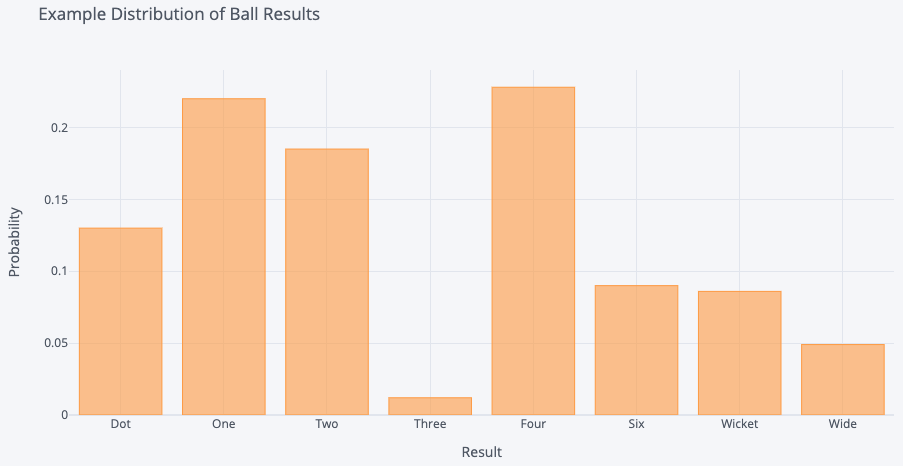
At the heart of this project is my ball prediction model which was trained on the ~700k balls in my dataset. This was a multi-class classification problem and for simplicity, I limited the classes (possible outcomes of a ball) to 8 options (0, 1, 2, 3, 4, 6, Wicket, Wide). The inputs to the model were:
- Match State:
- Innings
- Over
- Number of Runs
- Number of Wickets
- First Innings Score (if in second innings)
- Bowler Statistics (historical distribution of ball results across all balls that bowler has bowled)
- Batter Statistics (historical distribution of ball results across all balls that batsman has faced)
The output from the model was the predicted probability of each of the 8 possible ball results. In the simulation stage, we run the inputs for every ball through the model and then sample from this predicted probability distribution.
I won't go into too much detail about model choice and hyperparameter optimisation here since it is not the focus of this article but I have included the Keras summary of my final model below. In short, I trained a feed-forward neural network model with 2 dense layers of 50 nodes with a ReLU activation function on each. I also applied Batch Normalisation and Dropout.
Model: "sequential_4"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_12 (Dense) (None, 50) 1150
_________________________________________________________________
batch_normalization_8 (Batch (None, 50) 200
_________________________________________________________________
re_lu_8 (ReLU) (None, 50) 0
_________________________________________________________________
dropout_8 (Dropout) (None, 50) 0
_________________________________________________________________
dense_13 (Dense) (None, 50) 2550
_________________________________________________________________
batch_normalization_9 (Batch (None, 50) 200
_________________________________________________________________
re_lu_9 (ReLU) (None, 50) 0
_________________________________________________________________
dropout_9 (Dropout) (None, 50) 0
_________________________________________________________________
dense_14 (Dense) (None, 8) 408
=================================================================
Total params: 4,508
Trainable params: 4,308
Non-trainable params: 200
_________________________________________________________________
# Simulation Engine
The next step was to build a simulation engine in Python that could be used to generate full matches using the ball prediction model. At a high level the steps to generate a simulation are:
- Create two lists of player IDs (one for each team).
- Instantiate two Team objects (defined below) using the team lists from Step 1. Also, pass relevant historical batting and bowling statistics for each team to this class.
- Instantiate a MatchSimulator object (defined below) using the two Team objects, the Ball Prediction model and venue information.
- Run the sim_match module of the MatchSimulator object created in Step 3. The simulation steps are:
- a. Each match begins with a simulated coin toss and the winning team chooses to bat or bowl.
- b. Simulate each ball by running the Ball Prediction model with the current match state and relevant bowler and batter stats as input. Take a random sample from the distribution output by the model and update the MatchSimulator and Team states as required (e.g. if the ball result is "3" then add 3 runs to the on-strike batter's score and his team's score, add 3 runs to the bowler's stats, rotate the strike to the other batter and increment the ball counter).
- c. Repeat Step 4b until the innings is complete.
- d. Repeat for the second innings.
- Return the simulated match and player statistics.
This is not a tutorial but I have included some of my code below to illustrate the mechanics of this simulation engine.
# Team Class
class Team:
def __init__(self, name, bat_order, bat_lookup, bwl_lookup, mtc_ply_df):
self.name = name # team name
self.bat_lookup = bat_lookup # batter stats dictionary
self.bwl_lookup = bwl_lookup # bowler stats dictionary
self.mtc_ply_df = mtc_ply_df # historical player statistic (pandas dataframe)
self.order = {i+1:x for i, x in enumerate(bat_order)} # batting order
self.p_header = ['W','0','1','2','3','4','6','WD']
# batting innings state
self.bat_extras = 0
self.bat_total = 0
self.bat_wkts = 0
# bowling innings state
self.bwl_extras = 0
self.bwl_total = 0
self.bwl_wkts = 0
# player match statistics
self.ply_stats = dict()
for i, ply in enumerate(bat_order):
self.ply_stats[ply] = {
'runs': 0,
'balls': 0,
'4s': 0,
'6s': 0,
'out': 0,
'overs': 0,
'maidens': 0,
'runs_off': 0,
'wickets': 0,
'wides': 0,
'bat_order': i+1,
}
# calculate historical average # overs bowled for each player
if ply in mtc_ply_df.player_id.unique():
self.ply_stats[ply]['ave_overs'] = self.mtc_ply_df[self.mtc_ply_df.player_id == ply].overs.mean()
elif (i+1 >= 7) and (i+1 <= 9):
self.ply_stats[ply]['ave_overs'] = 2.5
elif (i+1 >= 10):
self.ply_stats[ply]['ave_overs'] = 4
else:
self.ply_stats[ply]['ave_overs'] = 0
# initialise team state
self.onstrike = self.order[1]
self.offstrike = self.order[2]
self.bowler = self.nxt_bowler(first_over=True)
self.bat_bwl = ''
def get_probs(self, pid, stats):
# module to return historical stats for a given player
if stats == 'bat':
if pid in self.bat_lookup:
ps = self.bat_lookup[pid]
else:
ps = self.bat_lookup['unknown']
elif stats == 'bwl':
if pid in self.bwl_lookup:
ps = self.bwl_lookup[pid]
else:
ps = self.bwl_lookup['unknown']
else:
return None
return [ps[x] for x in self.p_header]
def nxt_bowler(self, first_over=False):
# module to choose next bowler
if first_over:
lst_bwler = ''
else:
lst_bwler = self.bowler
pids = []
probs = []
for pid in self.ply_stats:
if (pid != lst_bwler) and (self.ply_stats[pid]['overs'] < 4):
pids.append(pid)
probs.append(self.ply_stats[pid]['ave_overs'])
return np.random.choice(a=pids, size=1, p=np.array(probs)/sum(probs))[0]
def wicket(self):
# module for updating the team after a wicket
self.bat_wkts += 1
self.ply_stats[self.onstrike]['out'] = 1
if self.bat_wkts < 10:
self.onstrike = self.order[self.bat_wkts + 2]
def new_over(self):
# module to start a new over
if self.bat_bwl == 'bat':
self.change_ends()
elif self.bat_bwl == 'bwl':
self.bowler = self.nxt_bowler()
self.ply_stats[self.bowler]['overs'] += 1
def change_ends(self):
# module to change the on-strike batter between overs
temp = self.onstrike
self.onstrike = self.offstrike
self.offstrike = temp
# Match Simulation Class
class MatchSimulator:
def __init__(self, t1, t2, ground, model, ave_score=160, verbose=False, pid2pname=None):
self.t_bat = t1 # batting team
self.t_bwl = t2 # bowling team
self.model = model # ball prediction model
self.verbose = verbose # flag to run simulation in verbose mode
self.pid2pname = pid2pname # dictionary mapping player ids to player names (for running in verbose mode)
self.res_opts = ['res_0', 'res_1', 'res_2', 'res_3', 'res_4', 'res_6', 'res_W', 'res_WD'] # list of ball result options
self.ave_score = ave_score # average first innings score at venue
# initialise match state
self.innings = 1
self.over = 0
self.ball = 0
self.comm = []
self.winner = ''
def sim_match(self):
# module to simulate match
if self.winner == '':
self.toss()
if self.verbose:
print()
print('%'*30)
print('1ST INNINGS')
print('%'*30)
while (self.over < 20) and (self.t_bat.bat_wkts < 10):
self.sim_over()
if self.verbose:
print()
print('Final Score: {}/{} off {}.'.format(self.t_bat.bat_wkts, self.t_bat.bat_total, self.over))
self.change_inns()
if self.verbose:
print()
print('%'*30)
print('2ND INNINGS')
print('%'*30)
while (self.over < 20) and (self.t_bat.bat_wkts < 10) and (self.t_bat.bat_total <= self.t_bwl.bat_total):
self.sim_over()
if self.t_bat.bat_total > self.t_bwl.bat_total:
self.winner = self.t_bat.name
elif self.t_bat.bat_total < self.t_bwl.bat_total:
self.winner = self.t_bwl.name
else:
self.winner = 'Tie'
if self.verbose:
print()
print('Final Score: {}/{} off {}.'.format(self.t_bat.bat_wkts, self.t_bat.bat_total, self.over))
print()
print('~'*20)
if self.winner != 'Tie':
print('{} WIN!'.format(self.winner))
else:
print('TIE!')
print('~'*20)
return [self.winner,
[self.t_bwl.name, self.t_bwl.bat_total, self.t_bwl.bat_wkts, self.t_bwl.ply_stats],
[self.t_bat.name, self.t_bat.bat_total, self.t_bat.bat_wkts, self.t_bat.ply_stats]
]
else:
print('Simulation already run.')
if self.winner != 'Tie':
print('{} won!'.format(self.winner))
else:
print('TIE!')
def sim_ball(self):
# module to simulate a ball
# get model inputs from match state
bowler = self.t_bwl.bowler
batter = self.t_bat.onstrike
bwl_stats = self.t_bwl.get_probs(bowler, 'bwl')
bat_stats = self.t_bat.get_probs(batter, 'bat')
inn = [self.innings == 2]
if self.innings == 1:
inn1_score = 0
else:
inn1_score = self.t_bwl.bat_total
mod_in = np.array(inn + [self.t_bat.bat_wkts/10, self.t_bat.bat_total/200, self.ave_score/200, inn1_score/200, self.over/20] + bwl_stats + bat_stats)
# predict ball result
res_probs = self.model(np.expand_dims(mod_in, axis=0))[0]
# sample from predicted distribution
res = np.random.choice(a=self.res_opts, size=1, p=np.array(res_probs))[0]
# increment balls faced for batter
self.t_bat.ply_stats[self.t_bat.onstrike]['balls'] += 1
# update match and team state based on ball result
if res == 'res_0':
self.ball += 1
elif res == 'res_1':
self.ball += 1
self.t_bat.ply_stats[self.t_bat.onstrike]['runs'] += 1
self.t_bwl.ply_stats[self.t_bwl.bowler]['runs_off'] += 1
self.t_bat.bat_total += 1
self.t_bwl.bwl_total += 1
self.t_bat.change_ends()
elif res == 'res_2':
self.ball += 1
self.t_bat.ply_stats[self.t_bat.onstrike]['runs'] += 2
self.t_bwl.ply_stats[self.t_bwl.bowler]['runs_off'] += 2
self.t_bat.bat_total += 2
self.t_bwl.bwl_total += 2
elif res == 'res_3':
self.ball += 1
self.t_bat.ply_stats[self.t_bat.onstrike]['runs'] += 3
self.t_bwl.ply_stats[self.t_bwl.bowler]['runs_off'] += 3
self.t_bat.bat_total += 3
self.t_bwl.bwl_total += 3
self.t_bat.change_ends()
elif res == 'res_4':
if self.verbose:
print('\t4 to {}!'.format(self.pid2pname[self.t_bat.onstrike]))
self.ball += 1
self.t_bat.ply_stats[self.t_bat.onstrike]['runs'] += 4
self.t_bat.ply_stats[self.t_bat.onstrike]['4s'] += 1
self.t_bwl.ply_stats[self.t_bwl.bowler]['runs_off'] += 4
self.t_bat.bat_total += 4
self.t_bwl.bwl_total += 4
elif res == 'res_6':
if self.verbose:
print('\t6 to {}!'.format(self.pid2pname[self.t_bat.onstrike]))
self.ball += 1
self.t_bat.ply_stats[self.t_bat.onstrike]['runs'] += 6
self.t_bat.ply_stats[self.t_bat.onstrike]['6s'] += 1
self.t_bwl.ply_stats[self.t_bwl.bowler]['runs_off'] += 6
self.t_bat.bat_total += 6
self.t_bwl.bwl_total += 6
elif res == 'res_W':
if self.verbose:
print('\tWICKET! {} out, bowled {}.'.format(self.pid2pname[self.t_bat.onstrike], self.pid2pname[self.t_bwl.bowler]))
self.ball += 1
self.t_bwl.bwl_wkts += 1
self.t_bat.ply_stats[self.t_bat.onstrike]['out'] = 1
self.t_bwl.ply_stats[self.t_bwl.bowler]['wickets'] += 1
self.t_bat.wicket()
elif res == 'res_WD':
self.t_bwl.ply_stats[self.t_bwl.bowler]['runs_off'] += 1
self.t_bwl.ply_stats[self.t_bwl.bowler]['wides'] += 1
self.t_bat.bat_total += 1
self.t_bwl.bwl_total += 1
return res
def sim_over(self):
# module to simulate an over
if self.verbose:
print('{} to bowl. {}/{} after {}.'.format(self.pid2pname[self.t_bwl.bowler], self.t_bat.bat_wkts, self.t_bat.bat_total, self.over))
self.over += 1
score_holder = self.t_bat.bat_total
while (self.ball < 6) and (self.t_bat.bat_wkts < 10) and ((self.innings == 1) or (self.t_bat.bat_total <= self.t_bwl.bat_total)):
bwl = self.t_bwl.bowler
bat = self.t_bat.onstrike
res = self.sim_ball()
self.comm.append([self.innings, self.over, self.ball, bwl, bat, res[4:]])
self.ball = 0
if self.t_bat.bat_total == score_holder:
self.t_bwl.ply_stats[self.t_bwl.bowler]['maidens'] += 1
self.t_bat.new_over()
self.t_bwl.new_over()
def toss(self):
# module to simulate the coin toss
if np.random.uniform() > 0.5:
temp = self.t_bat
self.t_bat = self.t_bwl
self.t_bwl = temp
self.t_bat.bat_bwl = 'bat'
self.t_bwl.bat_bwl = 'bwl'
if self.verbose:
if np.random.uniform() > 0.5:
won_toss = self.t_bat.name
else:
won_toss = self.t_bwl.name
print('The {} have won the toss!'.format(won_toss))
print('{} will bat first. {} to bowl.'.format(self.t_bat.name, self.t_bwl.name))
def change_inns(self):
# module to swap bowling and batting sides after 1st innings
temp = self.t_bat
self.t_bat = self.t_bwl
self.t_bwl = temp
self.t_bat.bat_bwl = 'bat'
self.t_bwl.bat_bwl = 'bwl'
self.over = 0
self.ball = 0
self.innings = 2
if self.verbose:
print('The {} are going in to bat. {} to bowl.'.format(self.t_bat.name, self.t_bwl.name))
I also included functionality to run the simulation engine in "verbose" mode which outputs a running commentary of a match's progress. An example of running a single simulation in this mode is shown below.
# Running A Simulation
# initialise teams
t1 = Team(
name='Sydney Sixers', bat_order=t1_pids, bat_lookup=bat_lookup, bwl_lookup=bwl_lookup,
mtc_ply_df=mtc_ply_df
)
t2 = Team(
name='Brisbane Heat', bat_order=t2_pids, bat_lookup=bat_lookup, bwl_lookup=bwl_lookup,
mtc_ply_df=mtc_ply_df
)
# initialise match simulator
venue = 'Sydney Cricket Ground'
ms = MatchSimulator(
t1=t1, t2=t2, ground=venue, model=model, ave_score=ven_score_lookup[venue], verbose=True,
pid2pname=pid2pname
)
# run simulation
ms.sim_match()
# Example Output
The Brisbane Heat have won the toss!
Sydney Sixers will bat first. Brisbane Heat to bowl.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
1ST INNINGS
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
MJ Swepson to bowl. 0/0 after 0.
4 to JL Denly!
JK Lalor to bowl. 0/4 after 1.
4 to J Avendano!
4 to J Avendano!
Mujeeb Ur Rahman to bowl. 0/12 after 2.
4 to JL Denly!
6 to JL Denly!
JL Pattinson to bowl. 0/23 after 3.
WICKET! JL Denly out, bowled JL Pattinson.
WICKET! MC Henriques out, bowled JL Pattinson.
6 to DP Hughes!
BCJ Cutting to bowl. 2/31 after 4.
WICKET! J Avendano out, bowled BCJ Cutting.
MJ Swepson to bowl. 3/34 after 5.
JL Pattinson to bowl. 3/36 after 6.
Mujeeb Ur Rahman to bowl. 3/38 after 7.
4 to JC Silk!
BCJ Cutting to bowl. 3/46 after 8.
Mujeeb Ur Rahman to bowl. 3/52 after 9.
4 to JC Silk!
BCJ Cutting to bowl. 3/60 after 10.
WICKET! JC Silk out, bowled BCJ Cutting.
JK Lalor to bowl. 4/63 after 11.
MJ Swepson to bowl. 4/68 after 12.
JK Lalor to bowl. 4/74 after 13.
4 to DP Hughes!
JL Pattinson to bowl. 4/82 after 14.
6 to JR Philippe!
6 to JR Philippe!
MJ Swepson to bowl. 4/96 after 15.
4 to JR Philippe!
JK Lalor to bowl. 4/106 after 16.
4 to JR Philippe!
MJ Swepson to bowl. 4/114 after 17.
WICKET! JR Philippe out, bowled MJ Swepson.
BCJ Cutting to bowl. 5/118 after 18.
6 to DP Hughes!
4 to TK Curran!
Mujeeb Ur Rahman to bowl. 5/132 after 19.
6 to TK Curran!
Final Score: 5/144 off 20.
The Brisbane Heat are going in to bat. Sydney Sixers to bowl.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
2ND INNINGS
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
BJ Dwarshuis to bowl. 0/0 after 0.
4 to M Bryant!
4 to M Bryant!
TK Curran to bowl. 0/8 after 1.
BAD Manenti to bowl. 0/9 after 2.
WICKET! M Bryant out, bowled BAD Manenti.
BJ Dwarshuis to bowl. 1/13 after 3.
4 to SD Heazlett!
4 to SD Heazlett!
MC Henriques to bowl. 1/25 after 4.
WICKET! SD Heazlett out, bowled MC Henriques.
4 to BB McCullum!
4 to BB McCullum!
WICKET! BB McCullum out, bowled MC Henriques.
SA Abbott to bowl. 3/34 after 5.
4 to JA Burns!
BAD Manenti to bowl. 3/41 after 6.
4 to JA Burns!
TK Curran to bowl. 3/46 after 7.
6 to JA Burns!
BJ Dwarshuis to bowl. 3/57 after 8.
4 to CA Lynn!
4 to CA Lynn!
6 to CA Lynn!
WICKET! JA Burns out, bowled BJ Dwarshuis.
SNJ O'Keefe to bowl. 4/72 after 9.
WICKET! CA Lynn out, bowled SNJ O'Keefe.
BJ Dwarshuis to bowl. 5/76 after 10.
4 to BCJ Cutting!
SA Abbott to bowl. 5/83 after 11.
WICKET! BCJ Cutting out, bowled SA Abbott.
TK Curran to bowl. 6/87 after 12.
6 to JL Pattinson!
4 to JJ Peirson!
6 to JL Pattinson!
BJ Dwarshuis to bowl. 6/105 after 13.
6 to JL Pattinson!
6 to JL Pattinson!
BAD Manenti to bowl. 6/123 after 14.
4 to JL Pattinson!
TK Curran to bowl. 6/129 after 15.
6 to JL Pattinson!
WICKET! JJ Peirson out, bowled TK Curran.
MC Henriques to bowl. 7/137 after 16.
4 to JL Pattinson!
Final Score: 7/145 off 17.
~~~~~~~~~~~~~~~~~~~~
Brisbane Heat WIN!
~~~~~~~~~~~~~~~~~~~~
To make predictions, we use the simulation engine described above. Each simulation represents a single possible outcome but using Monte Carlo methods we are able to estimate the distribution of match results by simulating many times. To predict the probability of an outcome, simply count up all the simulations where that outcome occurred and divide by the total number of simulations. For example, if you simulated a match between the Sydney Sixers and the Melbourne Stars 1000 times:
- If the Sixers were the winner in 570 of the simulations, then the predicted probability of the Sixers winning is 0.57
- If Steve Smith scored the most runs in 237 of the simulations, then the predicted probability of Steve Smith being the highest run-scorer of the match is 0.237
# Results
So after all that, is my model actually any good? To try to answer this question I took 1126 historical matches from my dataset and simulated them 500 times each. Ideally you would simulate each match many more times than this but it was computationally impractical for this project. Due to the bottom-up nature of my model, there are actually numerous modes of appraisal, some of which I outline below.
# Simulation Realism
The first common-sense test was to see if the predicted matches looked realistic and fortunately they did. Remember that the matches are simulated using the Ball Prediction model and therefore we had no guarantees that the outputs would be sensible. For example, if the Ball Prediction model was performing poorly we might see batting teams getting bowled out too frequently or teams racking up astronomical scores.
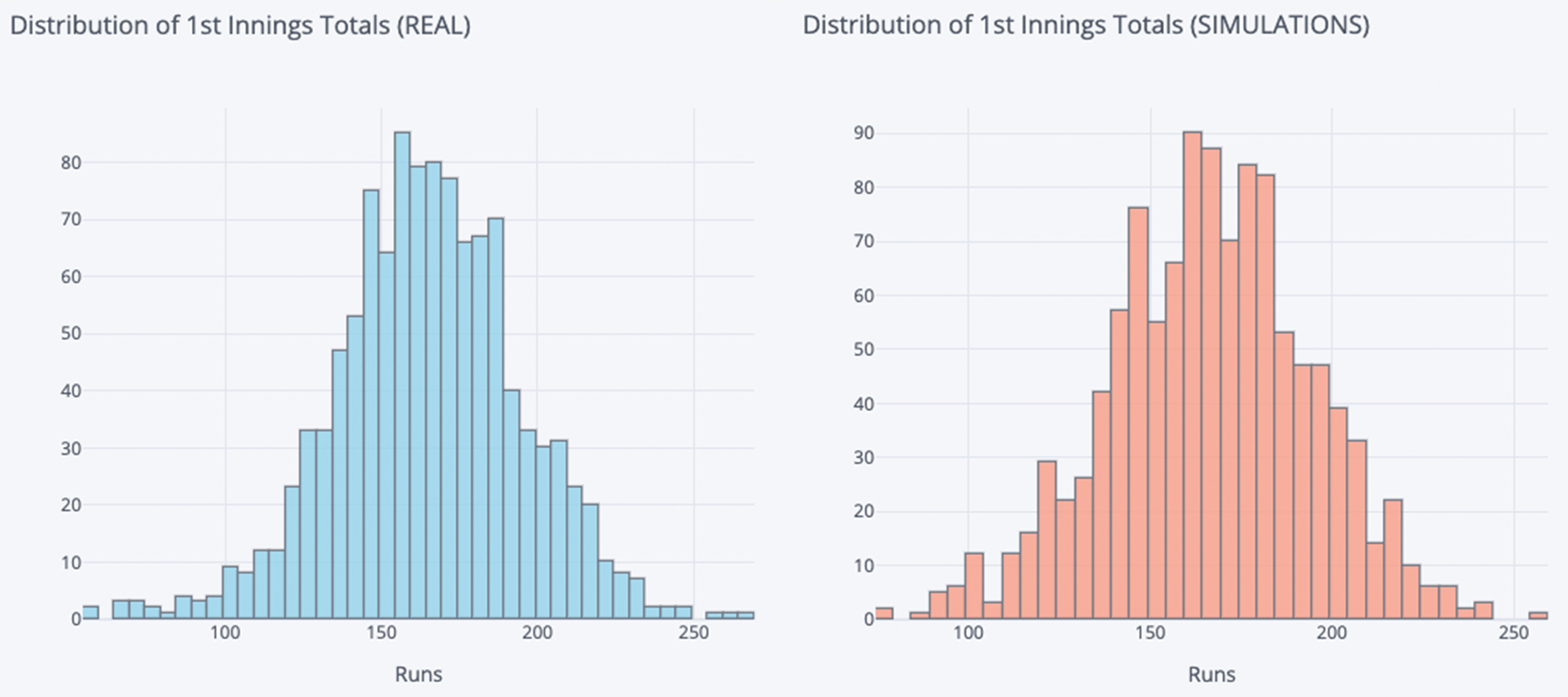
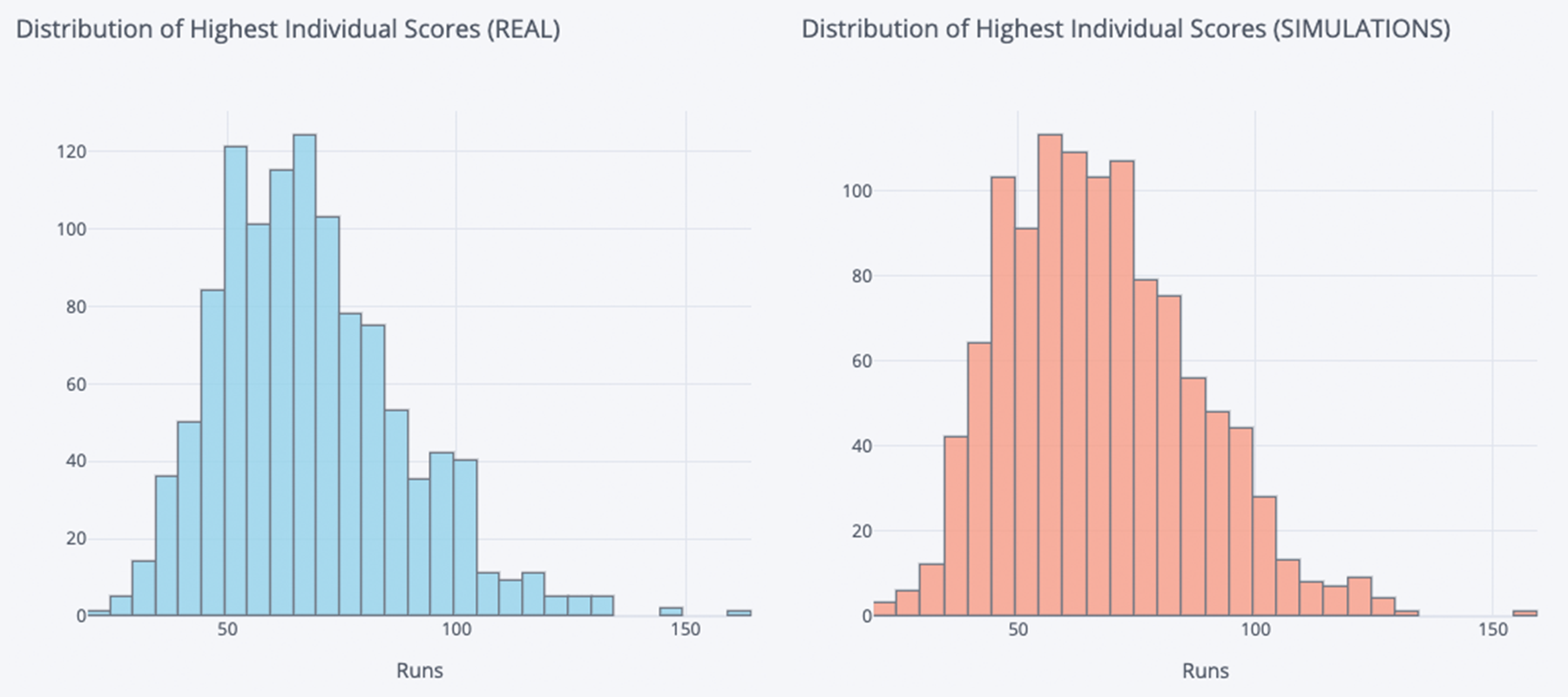
Having watched so much cricket in real life, I was able to quickly see that my simulations were reminiscent of real games, which was reassuring if not overly scientific. To further support my intuition, I sampled some real matches and simulations and compared the distributions of numerous match outcomes. In the examples below you can clearly see that the distributions for these outcomes are very similar for the real and simulated matches.
# First Innings Totals
# Match Wickets

# Highest Individual Scores
# Match Results
The next way I assessed my model was by predicting the winner of matches. As described earlier, to get the predicted probability of Team A winning Match X, simply add up all the simulations where Team A was the winner and divide by the total number of simulations. Across the simulated matches, my model was able to predict the winner with 55.6% accuracy and with a log loss of 0.687.
While I was initially quite underwhelmed by these results, I was buoyed by further analysis using historical betting odds from Bet365. When I compared my model predictions to the predictions implied by Bet365's odds I found that my model actually out-performed them. Bet365 picked the winner with lower accuracy (54.2%) and with a higher log loss (0.695). To put this in perspective, a benchmark model that predicts 0.5 probability for both teams for every match corresponds to a log loss of 0.693 meaning that the Bet365 odds are worse than a model with no information!
Now the take away here is not that my model is amazing at predicting T20 match results, but rather that T20 match results are inherently difficult to predict. I do suspect that I would get an uplift in model performance by simulating more than 500 times per match but I will need to test this hypothesis in future.
# Other Predictions
Finally, I tried predicting some other features of matches. Again I ran into the intrinsic unpredictability of the sport but I have included a few results below.
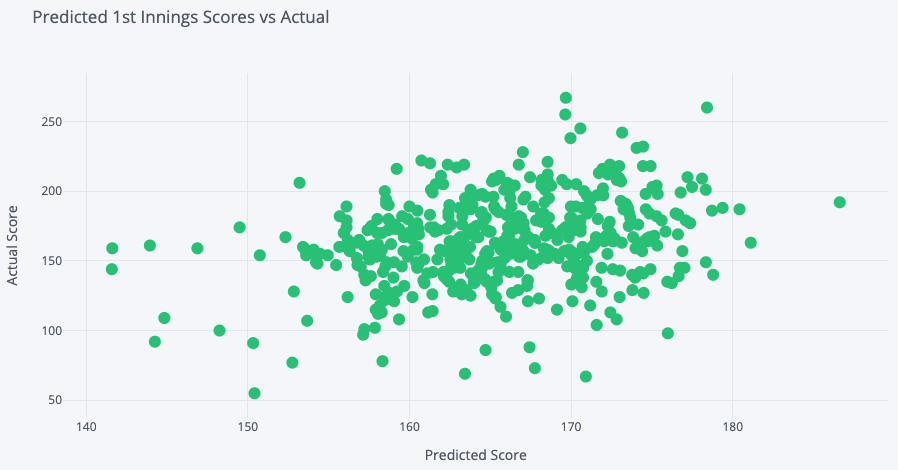
# First Innings Score
To predict the first innings score of each match I used the mean first innings score in all the simulations where the correct team batted first. In the scatter plot below we can see that there is a relationship between the predicted and actual scores but it is pretty noisy. The correlation here is 0.305 with a p-value of 1.18e-25 suggesting that the simulations are doing a reasonable job of modelling this feature but there are just too many unknowns to do it accurately. Further evidence for this is the average standard deviation for first innings score across all the simulated matches which was quite high at 28.6.
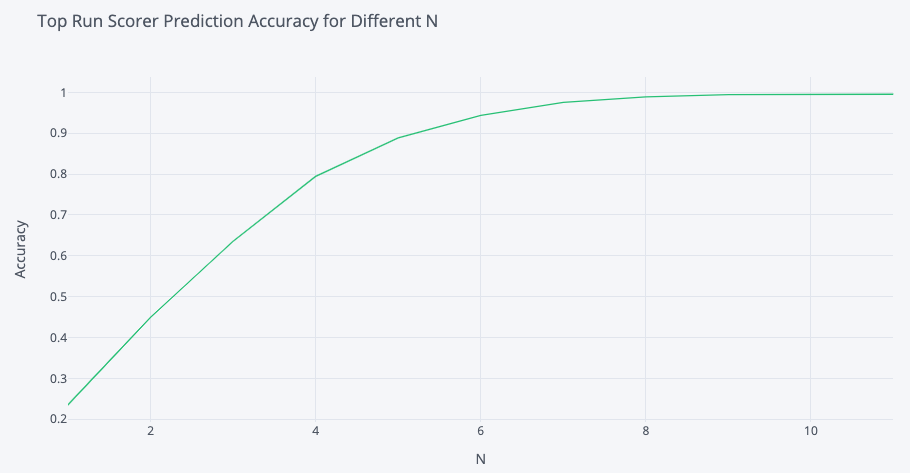
# Top Run Scorer
To predict the top run-scorer for a team in a given match, I chose the player who was the highest run-scorer in the most simulations. Using this method I was able to pick the highest run-scorer with ~25% accuracy. In the plot below we can see varying levels of accuracy when we choose the top N most likely highest run-scorers (rather than just the top 1). For example, in 80% of the matches I simulated, I had the true highest run-scorer in my top 4 predictions based on simulations.
# Top Wicket Taker
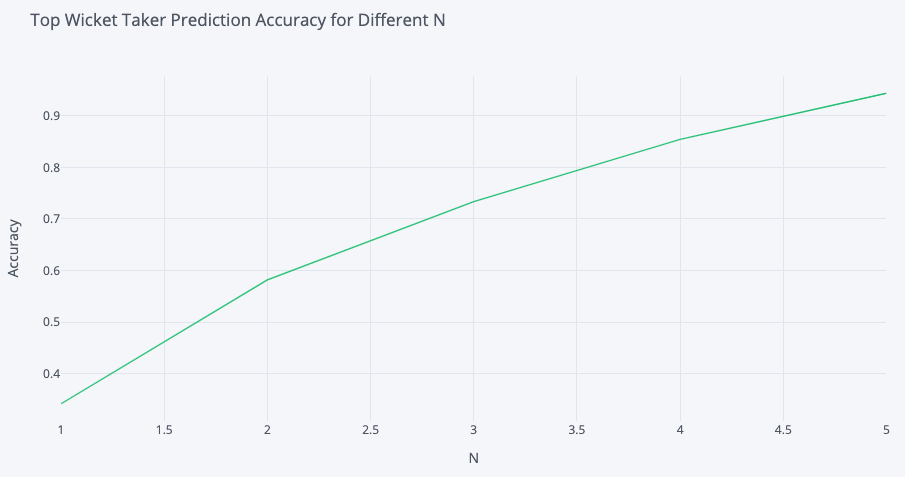
I used the same methodology here as for the Top Run Scorer prediction above but this time I was trying to pick the top wicket-taker for each team. The plot below shows that my top pick was correct in ~35% of matches and that the true top wicket-taker was in my top 3 predictions ~75% of the time.
# Conclusion
From the outset, the aim of this project was not really world-class prediction accuracy but rather to see if I could model whole T20 matches with ball-by-ball granularity, which I did. The model is very good at generating realistic simulations of T20 matches but unfortunately, it struggles to predict outcomes with much confidence. My intuition told me that this could be due to the sport just being difficult to predict in general and this was supported by my analysis of betting odds. I found that not only were the bookmaker's odds worse predictors than my model, they were even worse than a model with no information at all.
While this was a fun experiment, I discovered that there were some limitations to using it in practice. Firstly it takes a long time to run the simulations (approximately 10k simulations per hour on my machine). This wouldn't necessarily be a problem except for the fact that team lists are often not announced until 10-15 minutes before the game starts. Since one of the key advantages to the bottom-up style of modelling is the fact that it can better capture head to head matchups, simulating games with incorrect lineups is unlikely to yield good results.
In terms of next steps there are a few things I would like to try:
- Add more complexity to the ball prediction model. Because each simulation takes a relatively long time to run, I decided to keep my ball prediction model fairly light-weight, but I would like to experiment with adding more features.
- Try increasing the number of simulations per match. I did a small experiment with this and saw an immediate uplift in prediction accuracy so I would like to try simulating each match 10k+ times.
- Try building a similar model for a more predictable sport. The flexibility of this kind of modelling is very appealing and so I would like to try this bottom-up approach with a sport that is a bit easier to model.